Dall’inizio di marzo l’intera cittadinanza italiana è sottoposta a delle misure restrittive e di distanziamento sociale, che vietano qualsiasi uscita dalla propria abitazione che non sia giustificabile con motivi di estrema necessità, al fine di contenere l’epidemia da covid-19.

L’intento di questo articolo è quello di dare una lettura e una spiegazione, sia scientifica che politica, delle diverse misure attuate dal governo italiano, che riteniamo in alcuni punti insufficienti o addirittura ipocrite, nella battaglia alla diffusione del virus, il tutto a partire da una spiegazione dei modelli utilizzati per simulare le diffusioni epidemiche.

Data la sempre più distante percezione e fiducia che le classi popolari hanno verso le verità scientifiche e verso chi la scienza rappresenta, vorremo cercare di smontare questa barriera di classe, che troppe volte porta alla condivisione e/o nascita di fake-news. Riteniamo questo intervento estremamente necessario perché, in primo luogo, la scienza deve essere uno strumento a disposizione di ogni individuo e in secondo luogo ci muoviamo affinché sia possibile per tutti avere i mezzi per comprendere pienamente e analizzare criticamente i messaggi da cui siamo quotidianamente irrorati dai media.

Sottolineiamo fin da ora, che l’enorme variabilità della vita sociale non può essere ridotta ad una simulazione che identifica gli esseri umani come particelle in una scatola. Tuttavia questi modelli devono e possono servire per trarre alcune linee guida da utilizzare nella gestione dell’emergenza.

Ci preme iniziare spiegando perché, in assenza di restrizioni sociali, il numero di infetti di malattie virali aumenta esponenzialmente e quali possono essere le conseguenze di tale andamento.

Per farlo introdurremmo quello che in campo epidemiologico viene chiamato modello SIR, un modello utilizzato per simulare i possibili scenari e quali possano essere le possibili misure da prendere per arginare la diffusione virale.

Il modello SIR si basa sulla divisione della popolazione in tre gruppi, da cui si ricava l’acronimo del nome: il primo gruppo S sta per i Suscettibili e rappresenta la fetta di popolazione che può potenzialmente infettarsi; il secondo gruppo I sta per Infetti e rappresenta la fetta di popolazione attualmente infetta;  R invece sta per Recuperati (o più brutalmente Rimossi) che identifica la fetta di popolazione che o è guarita o è morta a seguito dell’infezione e quindi non può più trasmettere il virus né tanto meno ammalarsi di nuovo.

Una volta definiti i soggetti in gioco bisogna capire come avviene il contagio e trovare un modo per schematizzarlo. Quando una persona sana entra in contatto con una persona infetta non è detto che ci sia un contagio e quindi una diffusione del virus. Per questo motivo si introduce la probabilità che una persona suscettibile sia vittima dell’infezione. Questa probabilità è un parametro del modello che rappresenta le attività sociali dell’essere umano, come toccare le stesse superfici, stringersi la mano, baciarsi o starnutirsi addosso, etc. Quindi tanto più queste attività sociali sono presenti tanto più la probabilità sarà alta. Un altro parametro del modello è un raggio di interazione che schematizza il numero medio di incontri quotidiani tra le persone. Tanto più il raggio è grande tanto maggiore sarà il numero di persone con cui un individuo interagisce.

Definite le variabili attraverso cui in generale si può trasmettere il virus si possono inserire ulteriori parametri, ad esempio la presenza di luoghi sociali con un’alta concentrazione di persone, come luoghi di lavoro, scuole, supermercati e così via. È evidente, e può essere dimostrato con delle simulazioni, che l’introduzione di luoghi di interazione giochi un ruolo nella maggiore proliferazione della malattia virale. Per questo è fondamentale che tutti i luoghi non necessari per il benessere primario della collettività rimangano chiusi.

Questo approccio di tipo probabilistico supera inoltre la questione dei comportamenti individuali. Infatti, ci potranno essere persone molto ligie alle misure di prevenzione mentre altre che lo saranno meno, tuttavia quello che avrà un peso a livello collettivo sarà la media delle abitudini di prevenzione, non quello delle singole persone. Per questo motivo condanniamo la caccia all’untore e quindi la colpevolizzazione dei comportamenti individuali portata avanti da ogni televisione nazionale. Chi va a correre al parco ha un peso ed un effetto nettamente minore nella diffusione del virus rispetto alla presenza di luoghi centrali, come i poli produttivi, che convogliano ogni giorno migliaia di lavoratori e sui quali Confindustria fa orecchie da mercante.

Spieghiamo ora i vari tipi di andamento che può avere la diffusione di un virus. Innanzitutto, una crescita viene detta esponenziale se il numero sotto osservazione, in questo caso le persone infette, aumenta all’aumentare del tempo secondo una legge esponenziale I(t)=I(t₀ )e ^{f(R₀ )(t-t₀)}, il che significa che il numero cresce molto  velocemente. R₀ è il parametro chiave della funzione esponenziale e viene detto il “numero di riproduzione di base” che rappresenta il numero medio di infezioni secondarie prodotte da ciascun individuo infetto in una popolazione completamente suscettibile cioè mai venuta a contatto con il nuovo patogeno emergente. (…) Se l’R₀ di una malattia infettiva è circa 2, significa che in media un singolo malato infetterà due persone. Quanto maggiore è il valore di R₀ e tanto più elevato è il rischio di diffusione dell’epidemia. Se invece il valore di R₀ fosse inferiore ad 1 ciò significa che l’epidemia può essere contenuta. [1] Da delle prime osservazioni il valore di per il COVID19 è circa 2, ma si stima che in Lombardia prima delle misure contenitive fosse addirittura 4 [2] (per avere un metro di paragone quello dell’influenza stagionale è circa 1.3). Si comprende bene che per limitare un’infezione così virulenta a tutta la popolazione, che comporterebbe una saturazione del servizio sanitario nazionale ben peggiore di quello che stiamo osservando in questi giorni, gli sforzi maggiori vadano nella direzione di abbassare il valore di  al di sotto del valore 1, in modo tale da bloccare la diffusione dell’epidemia.

Per fare questo nelle simulazioni si variano i parametri da cui dipende l’evoluzione dell’epidemia, la probabilità di contagio, il raggio di interazione dei singoli individui e così via. Nella vita reale questo vuol dire applicare misure di distanziamento sociale, utilizzare dispositivi di prevenzione individuali e così via. Le simulazioni servono a ipotizzare quali siano gli scenari a seconda delle misure di contenimento prese in considerazione.

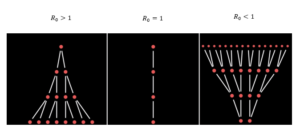
Fig. 1: Schema di diffusione della malattia in funzione del parametro R₀

Passiamo adesso a discutere i diversi scenari che possono essere investigati dalle simulazioni fatte a partire dal modello esemplificato in precedenza.Una delle prime conclusioni che si possono trarre dalle simulazioni è l’importanza della capacità di identificare e isolare i soggetti che hanno contratto il virus. Infatti, l’impossibilità di diffusione ulteriore, dopo un tempo breve dall’avvenuto contagio, dà vita ad una curva del numero di “infetti” con un picco estremamente ridotto ed un numero totale di persone che lo contraggono minimo rispetto ad altre misure adottabili. La simulazione, sia con l’isolamento del 100% dei casi sia con l’80% o il 50% (che tengono conto degli asintomatici), ci indica la necessità di rafforzare gli strumenti capaci di identificare e isolare i casi.

In sostanza quello che emerge è l’importanza di un sistema sanitario dotato di strutture territoriali diffuse capillarmente e capaci di effettuare tamponi domiciliari a tappeto e di processarli in laboratori di analisi locali. La trasformazione delle USL in ASL, la gestione aziendalistica, la competenza di gestione spostata sulle regioni e la dismissione di moltissime strutture locali avvenute negli ultimi trent’anni non consente oggi di adottare questa misura fondamentale, oltre ai danni evidenti sull’assistenza ordinaria. Se oggi per la risposta ad un tampone servono dai due ai sei giorni c’è una responsabilità politica chiara.

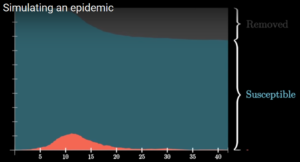Fig. 2: Caso in cui tutti gli infetti vengono tamponati e isolati

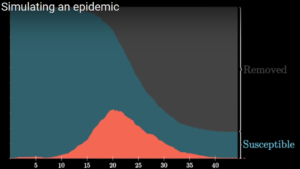Fig. 3: Caso in cui vengono tamponati e dunque isolati solo il 50% degli infetti

I due grafici in fig.2 e fig.3 mettono a confronto il caso in cui si riesca a isolare il 100% degli infetti con quello in cui si arrivi solo al 50% (entrambi considerano diverse comunità che interagiscono molto internamente e meno tra loro). È chiaro quindi quanto sia importante essere capillari ed efficaci nell’attuare una campagna di tamponamento a tappeto.

Un altro dei fattori che risultano dominanti nella diffusione dell’epidemia è la presenza nelle comunità di un “central hub”, ossia un polo frequentato periodicamente dalle persone come scuole, università, stazioni metro e soprattutto luoghi di lavoro ad alta densità. Infatti, la presenza di un polo attivo in una comunità risulta un fattore di diffusione disastroso anche se si applicano isolamento domestico e distanza sociale rispetto agli spostamenti “casuali”.

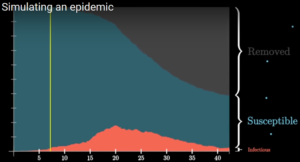
Fig. 4: Diffusione con central hub aperto e distanziamento sociale individuale attivo.

In fig.4 la linea verticale rappresenta l’inizio dei provvedimenti restrittivi che non comprendono però la chiusura del polo centrale per la comunità. La diffusione è ampia e si protrae con persistenza anche dopo il picco.

Per simulare la chiusura parziale di questi poli si può ridurre la frequenza di visita e quindi la probabilità che un membro della comunità vi si rechi. Possiamo così approssimare la condizione attuale, cioè quella di scuole, università e luoghi di aggregazione chiusi mentre i grandi centri produttivi e logistici sono aperti per reale necessità oppure per deroga prefettizia, fumosità delle categorie ritenute necessarie o controlli insufficienti. È utile anche confrontare, includendo in entrambi i casi le misure di restrizione degli spostamenti, l’effetto di una riduzione della frequentazione di questi poli con l’applicazione di misure igienico-sanitarie eccezionalmente stringenti ed efficaci.

Fig. 5: Pannello di sinistra, effetti della diminuzione della frequenza di visita ad un central hub di un fattore 5.
Pannello di destra, effetti della diminuzione della probabilità di contagio di un fattore 2.

Nel pannello sinistro di figura 5 la frequenza di visita è ridotta di un fattore cinque, mentre le migliori misure igieniche sono rappresentate nel pannello di destra con un dimezzamento della probabilità di contagio quando si entra a contatto con un soggetto infetto. Nonostante la restrizione sia più forte nel caso della frequenza di visita le due curve sono quasi sovrapponibili, è quindi lecito dedurne che il ruolo del polo sia dominante persino rispetto alla probabilità di infezione! Insomma mantenere aperte fabbriche che non siano strettamente indispensabili non è un fattore secondario ma un vero veicolo di diffusione che amplifica la portata dell’epidemia [3]. Tuttavia questa considerazione non vuole sminuire le norme igienico-sanitarie, che anzi devono essere stringenti per tutelare la salute di tutti quei lavoratori che non potrebbero comunque rimanere a casa.

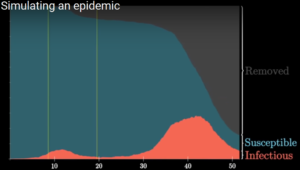
Fig. 6: effetti dell’allentamento anticipato delle misure restrittive.

Il governo ha tutti gli strumenti per fare valutazioni di questo tipo che si basino sui modelli esistenti di diffusione, eppure la scelta è quella di concedere ai padroni un enorme margine decisionale sul funzionamento degli stabilimenti. Anche gli appelli dell’Istituto Superiore di Sanità nel ritardare la riapertura dei luoghi di lavoro si scontra con le pressioni di Confindustria che vorrebbe invece un ritorno massiccio ai luoghi di lavoro già dopo Pasqua.

Infine qui si rappresenta la cessazione delle misure di isolamento e di quelle di restrizione sui poli con una seconda linea verticale. La lettura qualitativa delle conseguenze, anche tenendo conto di un certo mantenimento dell’isolamento domestico, è chiaramente quella di una nuova diffusione o comunque del prolungamento dell’epidemia.

Per concludere discutiamo gli effetti di una diffusione del contagio troppo repentina. In queste settimane, si è sentito parlare spesso di un fantomatico picco da raggiungere e di come il raggiungimento di questo picco, che poi sarebbe il numero massimo di contagiati, sia correlato con una mortalità non tanto legata al virus, ma ad una saturazione delle strutture sanitarie nazionali. Spieghiamo meglio questo concetto aiutandoci con un grafico.

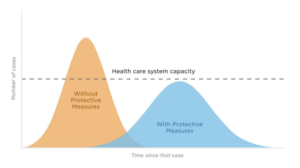
Nella figura sono presenti due curve; quella arancione che rappresenta un ipotetico andamento dei contagi nel caso in cui non vengano prese misure protettive per il contenimento del contagio stesso (guanti, mascherine, auto-isolamento, chiusura dei luoghi di assembramento…). Quella in blu invece rappresenta un altro ipotetico andamento dei contagi però nel caso in cui si siano prese misure di contenimento.

Le due campane gaussiane, sono poi messe a confronto con una linea orizzontale che rappresenta la soglia massima delle capacità di tenuta del sistema sanitario, che può essere approssimata banalmente al numero massimo di posti in terapia intensiva.

Il concetto che traspare è che avendo un numero limitato di posti letto nelle strutture ospedaliere per curare chi ne ha bisogno, tanto più i contagi giornalieri aumentano, cioè l’epidemia si diffonde rapidamente, tanti più saranno quei malati che necessiteranno contemporaneamente di cure in terapia intensiva. La crisi avviene quando il numero di malati gravi supera il numero di pazienti che il nostro sistema sanitario può assorbire. Le misure di prevenzione dunque, oltre a far diminuire in assoluto il numero di contagi, servono a far si che la curva dei contagi sia spalmata maggiormente nel tempo evitando così la saturazione dei posti letto.

Avere un certo numero di nuovi contagi in una settimana rispetto ad averlo in un giorno fa sì che gli ospedali, grazie alla dimissione dei pazienti già guariti, possano farsi carico di nuovi malati, evitando così la catastrofe per cui dei pazienti muoiano per il mancato accesso alle cure.

Da questa semplice immagine si evincono due aspetti. In primo luogo che i tagli sistematici al SSN hanno fatto sì che attualmente le strutture possano assorbire un numero minore di malati, abbassando sostanzialmente nel grafico la retta orizzontale e quindi facendo sì che il nostro sistema sanitario arrivi prima alla saturazione. In secondo luogo che chi, come Confindustria, ha spinto per ritardare la chiusura dei poli produttivi e ora gioca sui cavilli per continuare a rimanere aperto attraverso una ampia e poco veritiera concezione di bene di prima necessità, ha la responsabilità dei contagi dei propri dipendenti e la responsabilità nei confronti della società, perché hanno messo al primo posto i propri profitti piuttosto che il benessere collettivo.

In questo breve testo si è voluto mostrare come i modelli matematici di diffusione dell’epidemia possano darci delle indicazioni preziose su eventuali scenari futuri, e come determinate strategie possano influire la diffusione dell’epidemia. Come abbiamo visto le scelte politiche di questo governo, il ritardo nella chiusura di molti centri industriali non essenziali, l’ambiguità nella definizione stessa di produzioni necessarie e le deroghe per quelle escluse, rispondono agli interessi di Confindustria e dei padroni ignorando le strategie indicate scientificamente per il benessere della collettività.

Oggi è ancor più evidente come il modello produttivo, di sviluppo e di società capitalistici non siano razionali, non hanno una logica scientifica, a meno che essa non sia utile alle classi dominanti per fare maggiore profitto.

Ci troviamo qui di fronte alle contraddizioni del progresso tecnologico nel suo sviluppo in ambito capitalista. Le linee guida scientifiche vengono assunte a idoli sacri quando permettono di salvaguardare i profitti, altrimenti quegli avvertimenti rimangono prediche nel deserto.

Per approfondire la simulazione da cui sono ripresi i grafici, guarda il video: https://www.youtube.com/watch?time_continue=297&v=gxAaO2rsdIs&feature=emb_logo

Di Davide Tedeschi, Riccardo Beschi e Giacomo Maltempo

[1] Istituto superiore di sanità https://www.iss.it/primo-piano/-/asset_publisher/o4oGR9qmvUz9/content/id/5268851
[2] https://www.corriere.it/salute/malattie_infettive/20_marzo_28/coronavirus-perche-bisogna-puntare-ro-erre-zero-inferiore-1-e9ebe02c-70ca-11ea-a7a2-3889c819a91b.shtml
[3] https://www.lastampa.it/torino/2020/04/06/news/coronavirus-boom-di-contagi-negli-ambienti-di-lavoro-1.38687033